|
 Algebra help!
Algebra help!
#306027 - 03/20/13 12:15 PM
|
|
|
Multiply [3 + (2a + b)]²
Exactly what is says in the book. Even shows how to do it... but I don't understand it!
|
Just broke my personal record for number of consecutive days without dying!
|
|
|
 Re: Algebra help!
Re: Algebra help!
 [Re: URherenow]
[Re: URherenow]
#306028 - 03/20/13 12:28 PM
|
|
|
My guess
4a2+12a+4ab+3b+b2+18
No calculator used
Edited by DrLarryE (03/20/13 12:29 PM)
|
|
|
|
 Re: Algebra help!
Re: Algebra help!
 [Re: DrLarryE]
[Re: DrLarryE]
#306030 - 03/20/13 01:44 PM
|
|
|
I've forgotten it all but does the 3 still get distributed if there is a plus sign there? I don't think it does. I would guess
9 + 2a² + b²
|
|
|
|
 nope
nope
 [Re: DrLarryE]
[Re: DrLarryE]
#306031 - 03/20/13 01:44 PM
|
|
|
but what calculator could you have used anyway?
|
Just broke my personal record for number of consecutive days without dying!
|
|
|
|
[ATTACHED IMAGE - CLICK FOR FULL SIZE]

|
Just broke my personal record for number of consecutive days without dying!
|
|
|
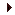 Re: What the book says (and I still don't understand at all)
Re: What the book says (and I still don't understand at all)
 [Re: URherenow]
[Re: URherenow]
#306033 - 03/20/13 02:01 PM
|
|
|
I forgot a lot of that. Do you have an actual instructor or you just have to learn from the book? I could never learn from the book in my college math classes, only learned from the teacher in class.
|
|
|
|
 Re: What the book says (and I still don't understand at all)
Re: What the book says (and I still don't understand at all)
 [Re: URherenow]
[Re: URherenow]
#306036 - 03/20/13 02:37 PM
|
|
|
OK I remember it now. Here is how you do it.
[3 + (2a + b)]²
first take out the brackets and the ² means multiply it by itself so
(3 + 2a + b)(3 + 2a + b)
Now you jump the multiplications, first take the first 3 and distribute it into each thing in the second parentheses then do the same with the 2a and b so
(3*3) + (3*2a) + (3*b) + (2a*3) + (2a*2a) + (2a*b) + (b*3) + (b*2a) + (b*b)
=
9 + 6a + 3b + 6a + 4a² + 2ab + 3b + 2ab + b²
then combine like terms
9 + 12a + 6b + 4a² +4ab + b²
|
|
|
|
 Re: Algebra help!
Re: Algebra help!
 [Re: URherenow]
[Re: URherenow]
#306037 - 03/20/13 03:05 PM
|
|
|
> Multiply [3 + (2a + b)]²
>
> Exactly what is says in the book. Even shows how to do it... but I don't understand
> it!
It's easy once you understand where the (a+b)^2=a^2+2ab+b^2 property is coming from.
First you have a layer of right/left distributivity:
(a+b)^2 = (a+b)(a+b) = a.(a+b) + b.(a+b) = aa + ab + ba + bb
(a+b+c)^2 = (a+b+c)(a+b+c) = a(a+b+c) + b(a+b+c) + c(a+b+c) = aa+ab+ac+ba+bb+bc+ca+cb+cc
What you get there is one term for every possible pair of letters, getting 4 of them for 2 initial terms, 9 for three, 16 for four, etc.
Now with the commutativity of multiplication and addition you can fold them together:
- for one letter, you get the pair with two times that letter once
- for two letters you get the pair twice, one in one order and the second the other way around (e.g. ab and ba)
So it generalizes as (a+b+...) = (sum of every term squared) + (sum of 2*every pair of terms in alphabetical order)
In the 3-term case that ends up (a+b+c)^2 = a^2+b^2+c^2+2ab+2ac+2bc
So (2a+b+3)^2 = 4a^2+b^2+9+4ab+12a+6b
Of course, that's not the way they want you to do it. They want you to take the (a+b)^2=a^2+2ab+b^2 as an article of faith, and use a extremely useful method called variable change to reuse it.
What is variable change, you ask? It just means that letters in an equation are just placeholders for whatever you want to put in them (hece the name variable, what they represent can vary). For clarity let's rewrite the equation as (X+Y)^2=X^2+2XY+Y^2.
You want to compute (3+(2a+b))^2, so you can say (and they didn't put the inner parenthesis there per chance):
X = 3
Y = 2a+b
The (3+(2a+b))^2 = (X+Y)^2, which you immediatly turn into X^2 + 2XY + X^2.
You can now substitute X and Y with the values you decided for them, giving:
(3+(2a+b))^2 = 3^2 + 2.3.(2a+b) + (2a+b)^2
Of course you're not going to stop it, so you can simplify and distribute once:
(3+(2a+b))^2 = 9 + 12a + 6b + (2a+b)^2
and the last term is yet another case of applying the property with X=2a and Y=b, giving
(3+(2a+b))^2 = 9 + 12a + 6b + (2a)^2 + 2.2a.b + b^2
(3+(2a+b))^2 = 9 + 12a + 6b + 4a^2 + 4ab + b^2
Which, oh wonder, is the same than the previous result.
OG.
|
|
|
| Hizzout |
|
70's baby, early 80's child
|
|
|

|
|
Reged: 02/05/04
|
|
Posts: 4841
|
|
|
|
|
|
Send PM
|
|
|
|
[ATTACHED IMAGE]

|
|
|
|
 Re: What the book says (and I still don't understand at all)
Re: What the book says (and I still don't understand at all)
 [Re: Smitdogg]
[Re: Smitdogg]
#306045 - 03/20/13 05:28 PM
|
|
|
> OK I remember it now. Here is how you do it.
>
> [3 + (2a + b)]²
>
> first take out the brackets and the ² means multiply it by itself so
>
> (3 + 2a + b)(3 + 2a + b)
>
> Now you jump the multiplications, first take the first 3 and distribute it into each
> thing in the second parentheses then do the same with the 2a and b so
>
> (3*3) + (3*2a) + (3*b) + (2a*3) + (2a*2a) + (2a*b) + (b*3) + (b*2a) + (b*b)
>
> =
>
> 9 + 6a + 3b + 6a + 4a² + 2ab + 3b + 2ab + b²
>
> then combine like terms
>
> 9 + 12a + 6b + 4a² +4ab + b²
You can also arrange it in a grid like this:
3 2a b
---------------
3 | 9 | 6a | 3b |
---------------
2a | 6a | 4a²| 2ab |
---------------
b | 3b | 2ab| b² |
---------------
Then add up everything inside the grid.
Plain numbers: 9 = 9
Multiples of a: 6a + 6a = 12a
Multiples of b: 3b + 3b = 6b
Multiples of ab: 2ab + 2ab = 4ab
Multiples of a²: 4a² = 4a²
Multiples of b²: b² = b²
Grand total: 9 + 12a + 6b + 4ab + 4a² + b²
Edited by amused (03/20/13 05:32 PM)
|
|
|
| Dullaron |
|
Diablo III - Dunard #1884
|
|
|

|
|
Reged: 07/22/05
|
|
Posts: 6125
|
|
Loc: Fort Worth, Tx
|
|
|
|
Send PM
|
|
|
 Heh... I don't know any of that stuff.
Heh... I don't know any of that stuff.
 [Re: URherenow]
[Re: URherenow]
#306046 - 03/20/13 05:50 PM
|
|
|
I never did go that far in high school.
|
W11 Home 64-bit + Nobara OS / AMD Radeon RX 5700 XT / AMD Ryzen 7 3700X 8-Core 3.59 GHz / RAM 64 GB
|
|
|
 Re: What the book says (and I still don't understand at all)
Re: What the book says (and I still don't understand at all)
 [Re: Smitdogg]
[Re: Smitdogg]
#306051 - 03/20/13 11:54 PM
|
|
|
not really. It's distance learning so I have to e-mail to get help.
What she want me to do is use FOIL twice! Using it once still ends up with a squared binominal at the end, so I have to FOIL that one as well, then combine like terms...
I like that grid approach much better.
Thanks amused!
OG... you're a smart guy but I think you over-complicated it. I get what you're saying but my brain is bleeding now.
|
Just broke my personal record for number of consecutive days without dying!
|
|
|
 Re: nope
Re: nope
 [Re: URherenow]
[Re: URherenow]
#306053 - 03/21/13 01:41 AM
|
|
|
> but what calculator could you have used anyway?
HP-48G running MetaKernel/Erable
HP-49G with stock firmware (this one has step-by-step mode that shows working)
TI-92 with stock firmware
TI-89 with stock firmware
Probably more calculators by now
But all of those are banned in high school maths exams.
|
|
|
|
 Re: What the book says (and I still don't understand at all)
Re: What the book says (and I still don't understand at all)
 [Re: amused]
[Re: amused]
#306069 - 03/21/13 05:25 AM
|
|
|
|
|
|
 Re: nope
Re: nope
 [Re: Vas Crabb]
[Re: Vas Crabb]
#306070 - 03/21/13 05:34 AM
|
|
|
High school? Thought you'd know a bit about me by now. Been military for almost 19 years now...
This is in the first week of a College Algebra course. (yea, first week and I already have a headache)
|
Just broke my personal record for number of consecutive days without dying!
|
|
|
 Re: nope
Re: nope
 [Re: URherenow]
[Re: URherenow]
#306075 - 03/21/13 08:12 AM
|
|
|
> High school? Thought you'd know a bit about me by now. Been military for almost 19
> years now...
>
> This is in the first week of a College Algebra course. (yea, first week and I already
> have a headache)
Yeah, I know you're military, and I know it's college algebra, but the stuff you're doing was covered in high school maths when I was at school if you chose an advanced maths subject. I don't know if any of those calculators would be banned on examinations for you, because that varies so wildly between countries, and even between colleges within a country. So YMMV. The calculator I preferred for doing that kind of stuff is the HP-49G, it's been my trusty workhorse for years. There's an updated version, the HP-50G, but I haven't used one so it could have some severe shortcomings I don't know about.
|
|
|
|
 Re: What the book says (and I still don't understand at all)
Re: What the book says (and I still don't understand at all)
 [Re: URherenow]
[Re: URherenow]
#306077 - 03/21/13 11:46 AM
|
|
|
> OG... you're a smart guy but I think you over-complicated it. I get what you're
> saying but my brain is bleeding now.
If you got what I was saying, you got _why_ it's working that way. And if you got that, after a short while you'll find out all the other manipulations to be trivial. That level of algebra is pretty much always the same thing.
OG.
|
|
|
|
 Re: nope
Re: nope
 [Re: Vas Crabb]
[Re: Vas Crabb]
#306088 - 03/21/13 05:05 PM
|
|
|
both of those look pretty cool (and useful and almost definitely not allowed) Won't go out of my way to order one but I'll keep an eye out and grab one if I see one.
Thanks 
|
Just broke my personal record for number of consecutive days without dying!
|
|
|
 Re: Algebra help!
Re: Algebra help!
 [Re: URherenow]
[Re: URherenow]
#306093 - 03/21/13 08:19 PM
|
|
|
What they are trying to teach you is formula substitution.
Think of A^2 + B^2 = C^2
But what if A is a formula? Something like A = (z^2 + 99) * 33. You can take the whole formula and stick it into the 'a' spot.
Now to really cook your noodle. B and C can be 'sub' formulas too.
Most algebra is about simplification into things you already know. FOIL/reduction/etc...
This is a technique that is used to help you simplify things for a little bit to change the way the formula looks. Then near the end you plug all the goop back in and it is easier to solve it. Pay attention to this trick in calc, linear alg, and stats, they *will* use it. And expect you to have just 'picked it up'.
Compilers use these sorts of things to help with optimization.
|
|
|